函数

特性

• 函数声明提升

静态方法

xxx.prototype 在 constructor 里面就看到了，

函数声明提升

a();
const a = function () {
  console.log('aaa');
};
function a() {
  console.log('bbb');
}
a();

一种危险的函数使用

为什么说它危险？

应该使用函数表达式

if (true) {
  function say() {
    console.log('hi');
  }
} else {
  function say2() {
    console.log('no hi!');
  }
}

递归

---

以下来自红宝石：

• 使用 arguments.callee，指向正在执行函数的指针

function factorial(num) {
  if (num <= 1) {
    return 1;
  } else {
    return num * factorial(num - 1);
  }
}
// ①如果设置中途转了一层
var authorFactorial = factorial;
factorial = null;
console.log(authorFactorial(4)); //error
// ② 上面可以变为
function factorial1(num) {
  if (num <= 1) {
    return 1;
  } else {
    return num * arguments.callee(num - 1); //但是在严格模式下，无法访问这个属性，所以会导致错误
  }
}
// ③ 更有效的方案，匿名函数的方式
var factorial2 = function f(num) {
  if (num <= 1) {
    return 1;
  } else {
    return num * f(num - 1);
  }
};

---

以下来自自己的摸索和总结：

函数自己调用自己,就是递归，由于递归需要具备超前的临时计算能力，对于我来讲，是很难一个学习难点。随后在网络上找到一个方法、函数来加深理解。

// 用递归 来求 5 的阶乘 ，翻译过来就是 1*2*3*4*5 =120
// n! = n * (n-1)!

// 定义一个函数，用于求 n 的阶乘
function func(n) {
  if (n === 1) {
    return 1;
  }

  // func(n-1) 因为传递的参数是 n-1,那么就是求 (n-1) 的阶乘
  return n * func(n - 1);
}
console.log(func(5));

// 所以计算的结果是
// 第一步 return 5 *(func(4))
// 第二步 return 5 *(4*(func(3)))
// 第二步 return 5 *(4*3*2(func(2)))
// 第二步 return 5 *(4*3*2(*1*func(1)))
// 第二步 return 5 *(4*3*2*1) = 120

再看一个斐波那契数列的递归数列，加深对递归概念的理解，小于 2 则 return 1，公式 f[n]=f[n-1]+f(n-2) 递归结束条件 f[1]=1;f[2]=1

• 基本规则

序列	值
0	1
1	1
2	2
3	3
4	5
5	8
6	13
7	21
8	34
9	55

/**
 * @desc for 循环实现 ，借用三个变量来存放
 * */
var fibFor = function (n) {
  let n1 = 1,
    n2 = 1,
    n3 = 0;
  if (n < 2) {
    return 1;
  }
  for (let i = 0; i < n - 1; i++) {
    n3 = n1 + n2;
    n1 = n2;
    n2 = n3;
  }
  return n3;
};
console.info(fibFor(9));

/**
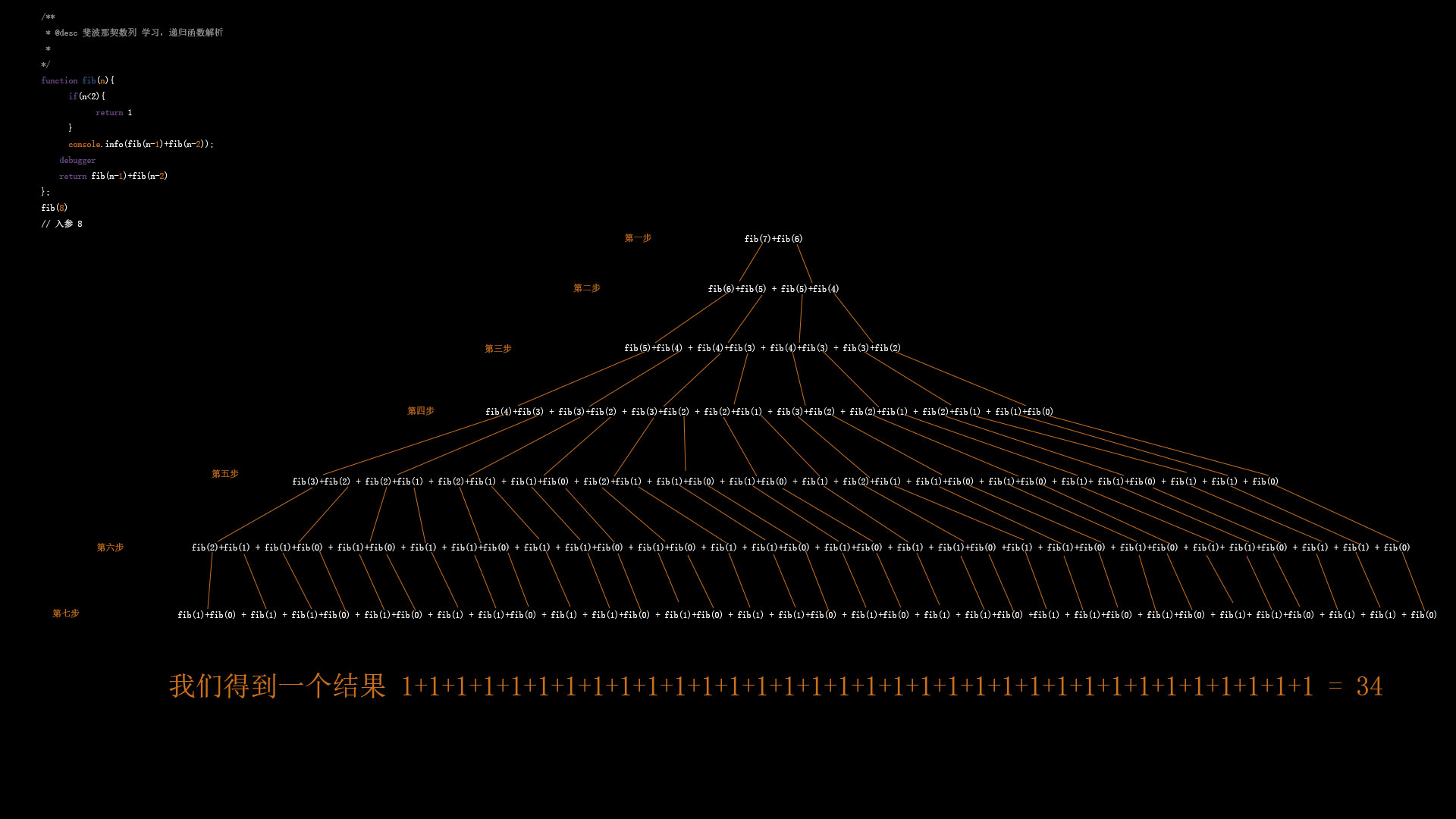
 * @desc 斐波那契数列 学习，递归函数解析
 *
 */
var fib = function (n) {
  if (n < 2) {
    return 1;
  }
  return fib(n - 1) + fib(n - 2);
};
console.info(fib(9));
fib(8);
// 入参 8

序列	值
第一步	fib(7)+fib(6)
第二步	fib(6)+fib(5) + fib(5)+fib(4)
第三步	fib(5)+fib(4) + fib(4)+fib(3) + fib(4)+fib(3) + fib(3)+fib(2)
第四步	fib(4)+fib(3) + fib(3)+fib(2) + fib(3)+fib(2) + fib(2)+fib(1) + fib(3)+fib(2) + fib(2)+fib(1) + fib(2)+fib(1) + fib(1)+fib(0)
第五步	fib(3)+fib(2) + fib(2)+fib(1) + fib(2)+fib(1) + fib(1)+fib(0) + fib(2)+fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1) + fib(2)+fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1)+ fib(1)+fib(0) + fib(1) + fib(1) + fib(0)
第六步	fib(2)+fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) +fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1)+ fib(1)+fib(0) + fib(1) + fib(1) + fib(0)
第七步	fib(1)+fib(0) + fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1) + fib(1)+fib(0) +fib(1) + fib(1)+fib(0) + fib(1)+fib(0) + fib(1)+ fib(1)+fib(0) + fib(1) + fib(1) + fib(0)
第八步	1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
第九步	去掉空格之后 我们得到一个结果 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1 = 34

立即执行

因为立即执行函数和外部的全局作用域的命名空间不同，于是 name1 和 this.name1 属于不同的空间，私有命名空间

/*立即函数的几种声明方式 1  匿名函数包括在一个括号运算符*/
(function (test) {
  console.log(test);
})(123)(
  /*立即函数的几种声明方式 2  匿名函数跟一个效果好。并包括一个原算法*/
  (function (test) {
    console.log(test);
  })(123)
);

/*demo*/
var name1 = 'World!';
(function (window) {
  console.log(window.name1, this.name1, name1); //window,window,undefined
  if (typeof name1 === 'undefined') {
    var name1 = 'JACK';
    console.log('hello,' + name1);
  } else {
    console.log('Goodbye' + name1);
  }
})(window);