算法

时间复杂度

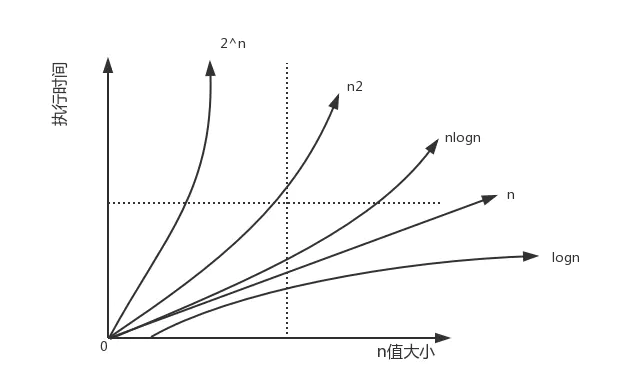
量级：

• 常数阶 O(1) ↓
• 对数阶 O(logN) ↓
• 线性阶 O(n) ↓
• 平方阶 O(n²) ↓
• 立方阶 O(n³) ↓
• K 次方阶 O(n^k) ↓
• 指数阶 O(2^n) ↓

越下面，执行的效率越低。

常数节：时间复杂度只有 O(1)

var a = 0;

var b = 0;

a++;

// or 此处的时间复杂度也是 O(n) 常数阶

function total() {
  let sum = 0;
  for (let i = 0; i < 100; i++) {
    sum++;
  }
}

// O(n2)

function total() {
  let sum = 0;
  for (let i = 0; i < 100; i++) {
    for (let j = 0; j < 100; j++) {
      sum++;
    }
  }
}

// 特殊的比较 O(m+n)，无法比较n 、m 大小

function total3(n, m) {
  let sum = 0;
  for (let i = 0; i < n; i++) {
    sum += i;
  }
  let sum2 = 0;
  for (let j = 0; j < m; i++) {
    sum2 += i;
  }
  return sum + sum2;
}

// 特殊的比较 O(n*m)
function total4(n, m) {
  let sumN = 0;
  let sumM = 0;
  for (let i = 0; i < n; i++) {
    sumN += i;
    for (let j = 0; j < m; j++) {
      sumM += j;
    }
  }
  return sumN * sumM;
}

线性阶 O(n):

对数阶 O(logN):

function total() {
  let sum = 0;
  let i = 1;
  while (i <= n) {
    sum += 1;
    i = i * 2;
  }
}

function total2() {
  let sum = 0;
  for (let i = 0; i < n; i = i * 2) {
    sum += 1;
  }
}

2x=n => x=log2n，这两者的时间复杂度为 O(log2n)

空间复杂度

空间复杂度：表示算法的存储空间和数据规模之间的关系

// 根据时间复杂度推算，忽略常数量级，每次数组都申请一个空间存储量，此时的空间复杂度为 O(n)
function initArray(n) {
  const arr = [];
  for (let i = 0; i < n; i++) {
    arr[i];
  }
}

0(1) 空间复杂度： O(n) 空间复杂度：

function total(n) {
  let sum = 0;
  for (let i = 0; i <= n; i++) {
    sum += i;
  }
  return sum;
}

total(10); //45

时间复杂度：O(n)，但是，显然这里的时间复杂度是高了。

// 通过调整算法后，时间复杂度仅为 0(1)
function total(n) {
  const sum = (n * (n + 1)) / 2;
  return n;
}

显然可以比较 O(n) > O(1)，这是算法的魅力，提高效率。 O(n2) 空间复杂度：